K-meansクラスタリングとDBSCAN クラスタリングの比較例 【Pythonコードとエルボー法も】

クラスタリングとは、ラベル付けされていないデータを次のようにグループ分けすることです。

同じグループのデータ点が互いに近接している
異なるグループのデータ点は互いに離れている

クラスター内の類似度が高く、クラスタ間類似度が低いように分けることが目的です。

クラスタリングには代表的な方法がいくつか知られていますが、この記事ではkmeans法を中心にしてクラスター数を自動で判定する方法も含めて紹介します。

k-means クラスタリング

k-meansクラスターは、最も一般的に使用されている教師なし機械学習クラスタリング技術の一つです。MacQueenによって1967年に命名された方法です。これはセントロイドベースのクラスタリング技法で、クラスタの数（セントロイド）を決定し、そのセントロイドをランダムに配置してスタートします。

k-means法のアルゴリズム

1. クラスターの数Kを決める。ランダムにK個の座標を生成し、最初のセントロイド (重心)とする。
2. 各点について、K個の各重心の間の距離を計算する。
3. 各点を最も近い重心に割り当てる。同じ重心に割り当てられた点は、同じクラスターを形成する。
4. クラスターが形成されたら、そのクラスターの平均を計算して新しい重心を求める。
5. 重心がそれ以上移動できなくなるまで、ステップ2, 3, 4を繰り返す。

なお、k-meansは昔から使われてきた有名な方法なので分かりやすい解説動画もいろいろYouTubeにあります。必要に応じて適宜ご覧ください。

k-means法の利点と欠点

k-meansのメリットとしては、理解しやすく実装しやすいとか、大規模なデータセットをうまく扱えるという点が挙げられます。

反対にデメリットとして、クラスター数Kを人が決めなければならず、その値によって大きく結果が変わることが挙げられます。他にも、外れ値との相性がよくない (中心点が外れ値に引っ張られ、クラスターが歪んでしまう)、次元数が増えるにつれて遅くなるなどの弱点があります。

k-means法をPythonで実装する

データサイエンス入門記事でよく使われているirisデータを使ってk-meansクラスタリングをしてみます。

k-means法はpython製の機械学習ライブラリであるscikit-learnに実装されているので、それを呼び出して使います。

まずは必要なライブラリなどと、今回のirisデータを読み込みます。

import pandas as pd
from sklearn import metrics
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

# irisデータの読み込みと表示
iris = load_iris()
iris.data

それではK-meansをやってみます。たった2行で終わります。

# K-meansをするためのインスタンスを作成。今回はクラスター数を3とする
iris_kmeans = KMeans(n_clusters=3)
# 作ったインスタンスにfitメソッドでデータを渡すだけ
iris_kmeans.fit(iris.data)

あとはpredictメソッドを使って各点がどのクラスターに所属するかを出力できます。

# 各点がどのクラスター (0, 1, 2) に所属するか
labels = iris_kmeans.predict(iris.data)
print (labels)

それぞれのクラスターごとに分かれているのか図示して確認してみます。

# クラスターごとに色をつけてプロット
plt.scatter(iris.data[:, 0], iris.data[:, 1], c=labels, cmap="rainbow")
plt.show()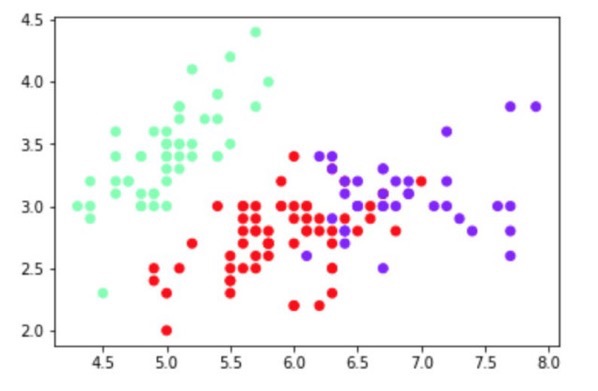

K-meansクラスタリングの結果、概ねきれいに分けることができました。

K-Meansの最適なクラスター数の探索法 (エルボー法)

K-Means法によるクラスタリング結果は、いくつのクラスターに分けるかというKの値に大きく依存します。それでは、どのようにしてKを選択すればよいのでしょうか？

一般的に使われているエルボー法 (Elbow Method) と呼ばれる手法を紹介します。

1. さまざまなKの候補の値について、まずK-Meansを行う。
2. 最終的にできたK個の各クラスターについて，所属する各点との距離の二乗和を計算する．
3. 各クラスターについてその値を足し合わせて、Kをその候補の値にしたときの二乗距離の合計を求める。
4. Kの値をX軸に、二乗和の合計をY軸にとったものをプロット
5. 曲線に急激な変化が起こるKを選択する (肘のように見える)。

これをコードで書くとこのようになります。

K = range(1,10)
sum_of_squared_distances = []

for k in K: # Kの値を1から9まで変化させてK-means法を行う
    model = KMeans(n_clusters=k).fit(iris.data)
    # クラスター内の二乗誤差を計算。実際には.inertia_にすでに計算済みなのでこれをリストに格納しておくだけ
    sum_of_squared_distances.append(model.inertia_) 
# さまざまなKにおける二乗誤差をプロットする
plt.plot(K, sum_of_squared_distances, "bx-")
plt.xlabel("K values")
plt.ylabel("Sum of Squared Distances")
plt.title("Elbow Method")
plt.show()

このプロットを見ると、K=3にエルボーがあることがわかり、これがこのデータセットに最適なクラスター数となります。

時には、エルボーが複数あることもあります。この場合、最適なKを見つけるために、シルエット係数 (Silhouette Coefficient) のような評価指標を使用したりします。シルエット係数が最も大きくなるKの値を選択します。

X-means法：k-meansの最適なクラスター数を提案する

K-means法の拡張として、クラスター数も自動的に提案してくれるX-means法というクラスタリング法もあります。

k-meansの繰り返しと、BIC（Bayesian information criterion）と呼ばれる情報量をベースにした分割停止基準を使って最適なクラスター数を決定する方法で、2000年に提唱されました。

アルゴリズム自体はpyclusteringというライブラリーに実装されていて、これを使うだけです。

使い方はこちらの記事などに詳しいです。

DBSCANクラスタリング

DBSCAN (Density Based Spatial Clustering of Applications with Noise) は、密度ベースのクラスタリング方法で、データ点の密集領域を1つのクラスターとし、逆に低密度の領域はノイズとみなすという手法です。です。

DBSCANのアルゴリズム

1. epsとminPtsの値を決めます。
eps (イプシロン) は、最大でどの程度離れた2点を同じクラスターに属するとみなすかを決めるパラメーターで、minPts (Minimum Points) はクラスターとみなすための最小限の点の数のことです (minPts未満の点しかない場合は、ノイズとして扱われます)。

2. 各点について、他のすべての点からの距離を計算し、もし距離が eps 以下ならば、その点を x に隣接する点としてマークする。その点が minPts 以上の隣接点がある場合には、クラスターとしてマークします。

3. この手順を繰り返すことでクラスタリングを行っていきます。

DBSCANのアルゴリズムは、図つきでDBSCANクラスタリングをPythonで行う方法 【scikit-learnによる実装コードあり】という記事で解説しているのでこちらも合わせてご覧ください。

DBSCANの利点と欠点

DBSCANには、外れ値を簡単に特定できノイズの多いデータセットに向いているとか、クラスターが不規則な形をしていてもよいというメリットがあります。

反対に、疎なデータセットではあまりうまく動作しないとか、epsやminPtsパラメータの影響を受けやすいという弱点もあります。

DBSCANをPythonで実装する

先ほどK-meansの時にも使ったirisデータセットを、今度はDBSCANでクラスタリングしてみます。

幸い、DBSCANもscikit-learnに実装されていて、ほとんど同じように実行することができます。

import pandas as pd
from sklearn import metrics
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt

iris_dbscan = DBSCAN(eps=0.5, min_samples=5)
iris_dbscan.fit(iris.data)
labels = iris_dbscan.labels_
print(labels)

このラベルは、0, 1,...であればそれぞれのデータ点が所属するクラスターを意味していて、-1であればノイズとみなされたということを意味しています。

DBSCANの最適なパラメーターepsの探索法 (ニー法)

DBSCANクラスタリングアルゴリズムは、パラメーターepsの値で結果が変わります。それでは、最適なeps値はどのように決めるのでしょうか？

これにはKnee methodとして知られる手法があります。全ての点について、K個の最も近い点 (K最近傍) との距離の平均を求め、グラフにして、最も急激な変化が起こる距離を選ぶというのが手法の概略です。

実際にやってみた方が分かりやすいかもしれません。Scikit-learnに入っているNearestNeighborsモジュールを使って最適なeps値の選択を示す例を示します。

from sklearn.neighbors import NearestNeighbors
nearest_neighbors = NearestNeighbors(n_neighbors=5)
nearest_neighbors.fit(iris.data)
distances, indices = nearest_neighbors.kneighbors(iris.data)
distances = np.sort(distances, axis=0)[:, 1]
print(distances)
plt.plot(distances)
plt.show()

最適なeps値は、最大曲率が見られる値、この場合は0.5に近いようです。

まとめに代えて

K-meansとDBSCAN、この2つのクラスタリング手法のどちらを使用するかは、解決したい問題によって異なります。生命科学研究では知名度の観点からK-meansが使われることが多いようですが、DBSCANを使用した方がより良いクラスタリングが得られる場合もあります。

さまざまなクラスタリング手法があることを知っておいて、必要な時に気軽に試せるようにしておくのがいいでしょう。

関連図書

この記事に関連した内容を紹介しているサイトや本はこちらです。

DBSCANクラスタリングをPythonで行う方法 【scikit-learnによる実装コードあり】

今日も【生命医学をハックする】 (@biomedicalhacks) をお読みいただきありがとうございました。当サイトの記事をもとに加筆した月2回のニュースレターも好評配信中ですので、よろしければこちらも合わせてどうぞ