PythonのSymPyで微分方程式を解く方法【ロトカヴォルテラを題材に】

Pythonは今やさまざまなところで使われていますが、生命科学においても大いに活用されています。
数値計算を簡単に行えるというのがPythonを科学研究に使うときの大きな長所なのですが、数値計算だけでなく数式展開もSymPyを使えば簡単に行なえます。

そこでこの記事では、SymPyで微分方程式を解く方法を、数理生物学の基本の1つであるロトカヴォルテラ方程式を題材にコード付きで紹介します。

この記事の内容

1 SymPyとロトカ・ボルテラのごく簡単な説明
2 連立方程式をSymPyで解く
3 ヤコビ行列をSymPyで求める
4 ヤコビ行列の固有値をSymPyで求める
5 平衡点近傍での挙動をSymPyで可視化する
6 まとめに代えて

SymPyとロトカ・ボルテラのごく簡単な説明

SymPyはPythonで数学計算を行うことができるライブラリーです。SciPyなど他のツールでも数値計算はできますが、SymPyの最大の特徴は数式として計算ができるということです。

同様のツールにはMathematicaなどが知られていますが、Mathematicaは高機能な分、高いライセンス料が必要です。

一方、SymPyは無料で利用でき、それでいて (少なくとも生命医学領域では) 十分な計算ができます。

この記事では、無料で利用できるウェブベースの計算環境である、Google Colaboratory (以下Colab) で動かしてみます。

ColabについてはGoogle Colaboratoryでデータサイエンスを始めよう【使い方入門】に簡単な紹介記事を書いているので、ご存知ない方はそちらをお読みください。

題材として利用するのは、捕食・被食の基本的な数理モデルであるロトカ・ボルテラモデルで、生命科学 x 数理科学の領域でよく入門書の題材として紹介されています。

数式ではこのように表されます。

ここでa, b, c, dはいずれも>0とします。

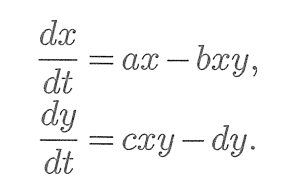
連立方程式をSymPyで解く

この常微分方程式は解析的に解くことはできません。
なので、線形安定性解析をしてその挙動を見ていきます。

まずは必要なツールをインポートします。

import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

from sympy.plotting import plot
sym.init_printing(use_unicode=True)
%matplotlib inline

# Google Colab 使用の場合、SympyによるTeX表示をサポートするために実行する
def custom_latex_printer(exp,**options):
    from google.colab.output._publish import javascript
    url = "https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.3/latest.js?config=default"
    javascript(url=url)
    return sym.printing.latex(exp,**options)

sym.init_printing(use_latex="mathjax",latex_printer=custom_latex_printer)

次に、モデルの変数と方程式を定義します。

# 変数，定数の宣言
sym.var('x,y,a,b,c,d')

# 関数f,gの定義
f = a*x - b*x*y
g = c*x*y - d*y

display(f)
display(g)

安定点は関数f=0, g=0の連立方程式の解になります。
SymPyでこれを解くためには、f=0, g=0を代入し、それをsympyのsolve関数に渡します。

eq1 = sym.Eq(f, 0)
eq2 = sym.Eq(g, 0)
equivs = sym.solve([eq1, eq2], [x,y])
display(equivs)

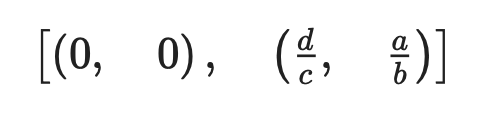
このように、この連立方程式には2つの解、 (0,0) と(d/c, a/b) があることが分かります。
これらがこの連立常微分方程式の平衡点ということです。

ヤコビ行列をSymPyで求める

この平衡点からほんの少しxやyがずれたら、どのようになるのでしょうか？
再びその平衡点に戻るのであれば、その平衡点は安定でロバストですが、そうではなく平衡点に戻らない場合、その平衡状態は不安定です。

これらを解析する方法の詳細は数理生物学の入門書に譲りますが、まず最初にやることは系を線形化したヤコビ行列を求めることです。

ごく簡単にいうと、2つの方程式のそれぞれをxないしyで偏微分し、その要素を並べてできたものがヤコビ行列です。

# ヤコビ行列の各要素を求める
j11 = sym.diff(f, x)
j12 = sym.diff(f, y)
j21 = sym.diff(g, x)
j22 = sym.diff(g, y)

# 要素を並べて行列にする
J =sym.Matrix(([j11,j12],[j21,j22]))
display(J)

ヤコビ行列の固有値をSymPyで求める

ヤコビ行列の後にやることは、それぞれの平衡点を代入し、その行列の固有値を求めることです。

まず平衡点 (0,0) での固有値を求めてみます。これはヤコビ行列にx=0, y=0を代入するだけです。
そうしてできた行列の固有値を求めればOKです。

実際にはこのようなコードで簡単に求められます。

u = sym.Matrix((x,y))

# 平衡点 (0,0) についての固有値
xy_equiv1 = list(zip(u,equivs[0]))
print(xy_equiv1)
display(J.subs(xy_equiv1))
ev1 = J.subs(xy_equiv1).eigenvals()
display(ev1)

{a: 1, -d:1}という辞書が出てきましたが、これはキーが固有値で、値が重複度を表しています。
つまりaという固有値が1つと、-dという固有値が1つあるということです。

今, aとdは正の値なので、このヤコビ行列は正の固有値 (a) を持つということを意味しています。

詳細は割愛しますが、平衡点が安定になるのは、この固有値の全てが負の場合です。
つまり、平衡点(0,0) が不安定であることがこの解析から簡単に分かります。

なお、より正確には1つの負の固有値と1つの正の固有値を持つので、(0,0) は鞍点という分類になります。

同じく平衡点 (d/c, a/b)について固有値を求めると、

# 平衡点 (d/c, a/b) についての固有値
xy_equiv2 = list(zip(u,equivs[1]))
print(xy_equiv2)
display(J.subs(xy_equiv2))
ev2 = J.subs(xy_equiv2).eigenvals()
display(ev2)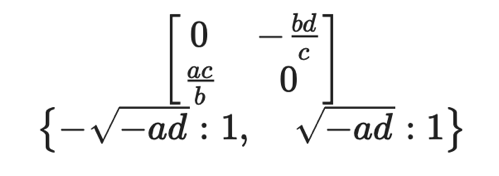

つまり± i sqrt(ad) となり、実部0の純虚数です。
このようなタイプは、中立安定と呼ばれます。

平衡点近傍での挙動をSymPyで可視化する

それでは実際に平衡点からちょっとxやyが変化したとき、その後どうなるのかを可視化してみます。
まず平衡点(0,0)から。この点は不安定 (正確には鞍点) であることがこれまでの解析から分かっています。

実際にベクトルで可視化してみます。

# 平衡点 (0,0) まわりの解の挙動
a_ = 1
b_ = 0.01
c_ = 0.02
d_ = 1

xo,yo = equivs[0]    # 平衡点
LX, LY = 0.05, 0.05  # 平衡点まわりの表示範囲（今回は±0.05の範囲を表示）
gridwidth = 0.01     # ベクトルを描画する間隔

x_array = np.arange(-LX+xo, LX+xo+0.001, gridwidth, dtype=float)
y_array = np.arange(-LY+yo, LY+yo+0.001, gridwidth, dtype=float)
X, Y= np.meshgrid(x_array, y_array)

# 解の挙動を算出
U = a_*X - b_*X*Y
V = c_*X*Y - d_*Y

# プロット
plt.figure(figsize=(4,4))
plt.quiver(X,Y,U,V,angles='xy',scale_units='xy', scale=5.0)
plt.savefig('vector1.eps')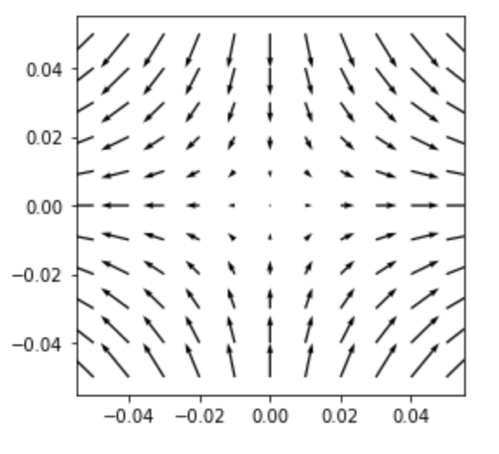

確かにちょっと動いたら不安定そうです。

もう1つの平衡点 (d/c, a/b) の周辺も調べます。
この場合、a, b, c, dの値によって平衡点が変わるので、適当に値を代入した上で可視化してみます。

# 平衡点 (d/c, a/b) まわりの解の挙動
a_ = 1
b_ = 0.01
c_ = 0.02
d_ = 1

xo,yo = equivs[1]    # 平衡点
xo = xo.subs(list(zip([c,d], [c_,d_])))  # パラメータの値を代入
yo = yo.subs(list(zip([a,b], [a_,b_])))  # 同上

LX, LY = 0.05, 0.05  # 平衡点まわりの表示範囲（今回は±0.05の範囲を表示）
gridwidth = 0.01     # ベクトルを描画する間隔

x_array = np.arange(-LX+xo, LX+xo+0.001, gridwidth, dtype=float)
y_array = np.arange(-LY+yo, LY+yo+0.001,gridwidth, dtype=float)
X, Y= np.meshgrid(x_array,y_array)

# 解の挙動を算出
U = a_*X - b_*X*Y
V = c_*X*Y - d_*Y

# プロット
plt.figure(figsize=(4,4))
plt.quiver(X,Y,U,V,angles='xy',scale_units='xy', scale=5.0)
plt.savefig('vector2.eps')

固有値が純虚数のとき「中立安定」と呼ばれる状態になります。
可視化してみると、平衡点から少し動いた時、平衡点に近づくことも離れていくこともないということが分かります。