Graph convolutionを数式を使わずに解説【グラフ畳み込みのPythonコード】

グラフ畳み込みニューラルネットワーク（GCN）は、画像解析で有名になった畳み込みニューラルネットワーク (CNN) のグラフ版です。

生命医学領域にはグラフで表現できるデータがたくさんあり、例えばタンパク-タンパク相互作用やシグナル伝達経路、あるいは創薬分野では薬そのものが元素が複雑につながったグラフとみなすことができます。

GCNについては日本語で読める書籍がほとんどなかったり、あるいは医学・生命科学系の研究者の多くには説明が難解すぎたりするので、この記事でグラフ畳み込みとは何かについて数式を使わないで解説します。

この記事の内容

1 グラフ畳み込みに必要なもの
2 グラフ畳み込みの原型
3 2つの問題を改良する
- 3.1 自分の情報がなくなってしまう
- 3.2 次数が高いノードほど、値が大きくなる
4 重みと活性化関数を追加してグラフ畳み込みの完成
5 全てをまとめてグラフ畳み込みを行う
6 まとめに代えて
7 関連図書

グラフ畳み込みに必要なもの

この記事を読んでいる方ならご存知だと思いますが、グラフは数学で出てくる図のことではなく、頂点 (Vertex, ノードともいう) とそれを結ぶ辺 (edge)からなっています。

話を簡単にするため、このようなシンプルなグラフを考えます。

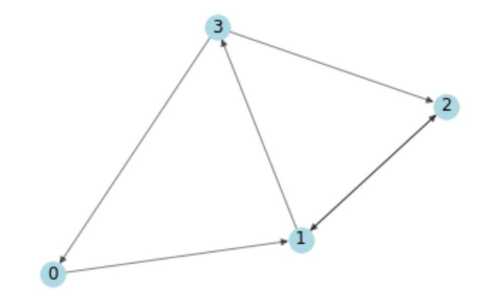
まずこのグラフの隣接行列が必要です。

隣接行列は、その頂点 (ノード) にどのノードが接続しているかを0 (つながっていない)か1 (つながっている) で表したものです。

例えば0番のノードを見てみると、そこからエッジが出ているのは1番のノードだけで、他の3つ (0, 2, 3番) には出ていません。したがって0番ノードは[0, 1, 0, 0]と表現できます。

同様に1番ノードは0と1番には出ておらず、2と3番にエッジがつながっているので[0, 0, 1, 1]です

NumPyを使えば、隣接行列Aをこのように実装できます。

import numpy as np

A = np.matrix([
    [0, 1, 0, 0],
    [0, 0, 1, 1], 
    [0, 1, 0, 0],
    [1, 0, 1, 0]],
    dtype=float
)

次に，各ノードの特徴量をまとめた特徴量行列Xが必要です。

ノード0、1、2、3それぞれを何次元かの数値ベクトルで表すのです。

実際は各ノードの特徴量はそれぞれ計算 (例えば炭素Cや水素Hを物理化学的な性質に基づいてベクトルで表現したり) するのですが、ここではデモ目的で後で手計算で確認できるように簡単な値を割り振っておきます。

X = np.matrix([
            [i, -i]
            for i in range(A.shape[0])
        ], dtype=float)
X

ここではノード0の特徴量を[0,0], ノード1の特徴量を[1, -1]のように表現してみました。

グラフ畳み込みの原型

隣接行列Aと入力特徴量Xをかけたらどうなるでしょう？

A * X

ここで結果をよく観察してみると、各ノード（各行）の表現は、そこに隣接するノードの特徴の総和になっていることに気がつきます。

例えば、ノード0はノード1と接続しているので、ノード1の表現である[1, -1]になっていますし、ノード1は接続するノード2 ([2, -2]) とノード3 ([3, -3]) の特徴量を足し合わせた[5, -5]ということです。

この計算 (グラフ畳み込み) により、各ノードをその近傍の特徴の総和として表現できることが分かりました (今回はエッジに向きがある有向グラフですが、向きのない無向グラフとして隣接行列を用意して無向グラフバージョンの畳み込みもできます)。

2つの問題を改良する

ここでちょっと問題が2点ありますので、これらを解決していきます

自分の情報がなくなってしまう

この計算をすると、ノード自身の特徴が含まれなくなってしまうのです。

そこで、各ノードに自分自身へのループを加えることにします。そうすれば自分のノードの情報を正しく受け継ぐことができます。

一般的には、これは隣接行列Aに単位行列Iを加えることで実現できます。

まずはAと同じサイズの単位行列Iを作ります。

I = np.matrix(np.eye(A.shape[0]))
I

隣接行列AにIを足すことで、各ノードに自分自身へのループを追加し (A_hat)、ここに前と同じように特徴量Xをかけてみます。

A_hat = A + I
A_hat * X

そうすると今度は自分自身の情報も加味した値になりました。例えばノード1は接続するノード2 ([2, -2]) とノード3 ([3, -3])、そして自分自身[1, -1]の特徴量を全て加算した[6, -6]になっています。

次数が高いノードほど、値が大きくなる

2つ目の問題は、次数の高い (たくさん接続している) ノードほど一般的には値が大きくなる一方で、次数の低いノードは特徴量の値が小さくなりがちだということです。

ニューラルネットワークにすると勾配消失や勾配爆発を引き起こす可能性があるので、単に特徴量を加算していくのではなく、一種の正規化が必要です。

これは一般には次数行列Dの逆行列をかけるということで対処できます。

次数行列は、核ノードがいくつのノードとつながっているか (次数) を対角行列の形で表したもので、対角成分以外は0になります。

今回の場合、ノード0と3が接続するのは1つ、ノード1と2が接続するのは2つなので、次数行列Dはこのように表現できます。

D = np.array(np.sum(A, axis=0))[0]
D = np.matrix(np.diag(D))
D

これの逆行列を隣接行列Aにかければいいのです。

もう一度Aを見ておきます。

Dの逆行列をAにかけると

D**-1 * A

隣接行列の各行の重み（値）が，その行に対応するノードの次数で割られていることを見てください。この変換された隣接行列を使って、特徴量行列Xとの演算をいつもどおり行います。

D**-1 * A * X

重みと活性化関数を追加してグラフ畳み込みの完成

ニューラルネットワークに必ず出てくる重みと活性化関数について、これまで触れていませんでしたが、ここで登場します。

D_hatを、A_hat = A + Iの次数行列、つまり強制的な自己ループを持つAの次数行列であるとします。これまで見てきた計算の最後に、重みWを掛け算します。

D_hat = D + np.eye (4)

W = np.matrix([
             [1, -1],
             [-1, 1]
         ])
D_hat**-1 * A_hat * X * W

ここでは重みWは2×2のサイズとしましたが、例えば2×1行列の重みを使えば最終的な出力が4×1になり、次元を削減することができます。

そして、ここに活性化関数を適用します。例えばReLUを使う場合、ReLU (D_hat**-1 * A_hat * X * W) を計算することになり、

[[1., 0.],
[4., 0.],
[2., 0.],
[5., 0.]]

という結果が得られます。これが、1つのグラフ畳み込み層でやっていることです。

全てをまとめてグラフ畳み込みを行う

それではこれまで紹介してきたことを全て使って簡単なグラフ畳み込みをやってみます。

ネットワーク分析によく使われるPythonパッケージnetworkxの中にあるkarate_club_graphのデータを使います。

ちなみにこんなネットワークです (詳細はいろいろなところで解説されているので割愛します)。

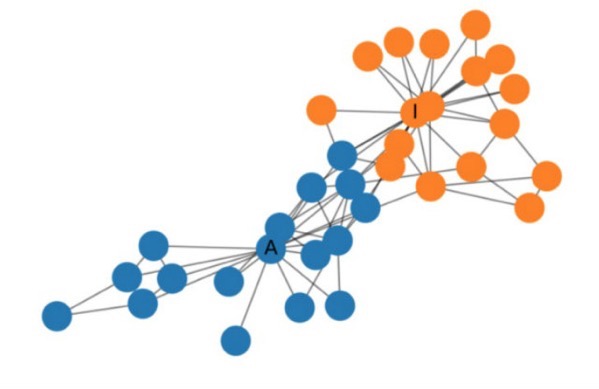
from networkx import karate_club_graph, to_numpy_matrix
zkc = karate_club_graph()
order = sorted(list(zkc.nodes()))

# 隣接行列
A = to_numpy_matrix(zkc, nodelist=order)
# 単位行列
I = np.eye(zkc.number_of_nodes())
# 自己ループをつけた隣接行列
A_hat = A + I
# 自己ループをつけた隣接行列の次数行列を作成
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.matrix(np.diag(D_hat))

次に重みを定義します。ここでは2回のグラフ畳み込みを行うことにしますので、重みも2つ必要です。1つ目は特徴量行列Xの各ノードの特徴量数x1回目の畳み込み後のノードの特徴量数で、2つ目は1回目の畳み込み後のノードの特徴量数 x 2回目の畳み込み後のノードの特徴量数のサイズです。

ここではそれぞれ1回目が4次元の特徴量ベクトル、2回目が2次元の特徴量ベクトルとし、それぞれ正規分布に従う乱数で初期化しました。

W_1 = np.random.normal(
    loc=0, scale=1, size=(zkc.number_of_nodes(), 4))
W_2 = np.random.normal(
    loc=0, size=(W_1.shape[1], 2))

グラフ畳み込み層の定義はもうこれまでに紹介しました。

def gcn_layer(A_hat, D_hat, X, W):
    return D_hat**-1 * A_hat * X * W

この実装では簡単にするため活性化関数は使っていませんが、実際にはReLUなり好みの活性化関数を通したものをreturnすることになります。

それではグラフ畳み込みを2回かけてみます。本当は特徴量ベクトルXを入力するのですが、ここでは簡単にするために単位行列Iを使っています。

H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2

どのような感じになったのかそれぞれのノードの値を見てみます。

feature_representations = {
    node: np.array(output)[node] 
    for node in zkc.nodes()}

このように、2回のグラフ畳み込みの結果、各ノードが2次元のベクトルで表されるようになりました。図示するとこのようになります。

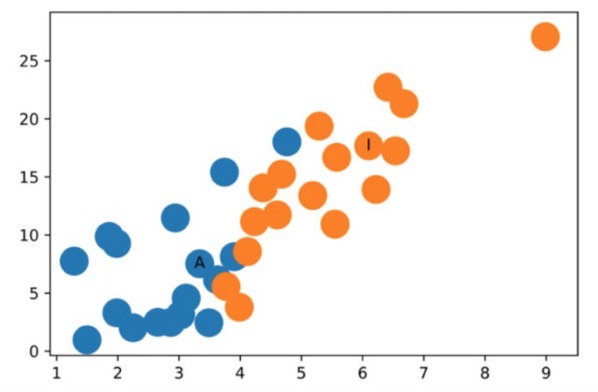
活性化関数すら使っていないのにグラフの大まかな構造をしっかり捉えられています。

まとめに代えて

この記事では「グラフ構造を畳み込む」とはどういうことかについて、数式を全く使わずに説明しました。このような畳み込みをたくさん重ねて、(CNNのように) 最終的にそれらをflattenなどで1つにまとめ、全結合層をさらに足していけばいわゆるグラフ畳み込みネットワーク (Graph Convolutonal Network, GCN)になります。

GCNは生命医学領域でも創薬関係やタンパク-タンパク結合ネットワークの解析など幅広い応用が期待されていて、今も新しいアプローチが盛んに研究されています。