感染症の広がりをシミュレーションするSIRモデルについて、感染症のSIRモデル入門編 【シミュレーションコードあり】という記事で具体例を出しながら紹介しました。
この記事では、もう少し複雑なモデルについてシミュレーションコードとともに紹介します。
この記事の内容
SIRモデルのおさらい
前回の記事で定義した変数はこちらです。
N: 集団の人口
S(t): day tにおける感染しうる (susceptibleな) 人の数
I(t): day tにおける感染している人の数
R(t): day tにおける感染後に回復した状態の人の数
β: 感染者1人が1日に病原体を広げてしまう人数
D: 感染が持続する日数
γ: 感染者のうち、その1日に回復する人の割合 (γ = 1/D)
R₀: the total number of people an infected person infects (R₀ = β / γ)
これらを使って、次の連立常微分方程式を実例とともに導出しました。
$\frac{dI}{dt} = \beta・I・\frac{S}{N} - \gamma・I$
$\frac{dR}{dt} = \gamma・I$
これらの方程式を導出するとき、直感的に翌日の人口に何が起こるかを教えてくれる「方向」として考えてきました。例えば、10人が感染し回復率が1/5(=γ)だった場合、翌日の回復者は10 * 1/5 = 2人増加するはずです。
あるコンパートメントS, I, Rから別のコンパートメントへの遷移を表すということです。この考え方は、より多くのコンパートメントを導入していくときにとても役に立ちます。
SIRモデルの箱を使った表現
コンパートメントはこのような箱です。
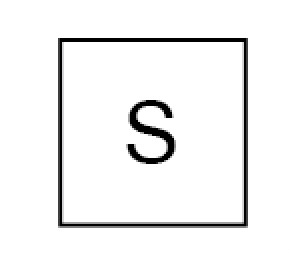
1つのコンパートメントから別のコンパートメントへの遷移を矢印で表し、次のように表示します。

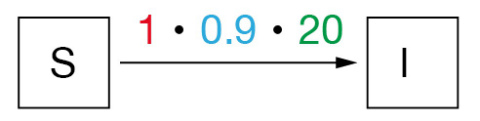
率rateは移行にかかる時間を表し、probabilityはある個人にこの移行が起こる確率、populationはこの移行が適用される集団の人数です。
例として、SIRの式のSusceptiblesからInfectedへの移行を見てみましょう。β=2、総人口100人、感染者10人、感受性90人だとします。
感染はすぐに起こるのでrateは1です。感染した10人がそれぞれ2人を感染させるので、移行が起こるpopulationは2 * 10 = 20人になります。Probabilityは0.9ですが、これは全集団100人のうちSusceptibleが90人いるからです。
モデル全体についてより一般的に書くと

(I → Rの場合、レートはγで、全員が回復するので確率は1)。
微分方程式との対応関係を見てみましょう。
$\frac{dI}{dt} = \beta・I・\frac{S}{N} - \gamma・I$
$\frac{dR}{dt} = \gamma・I$
コンパートメントに向かっていく矢印は式の中で加算され,コンパートメントから離れていく矢印は減算されることが分かると思います。
SIRモデルの改良
多くの感染症には、病原体が十分増殖するまでの潜伏期間があり、その間は感染を広めないことにします。このような状態にある人をまとめるExposeコンパートメントを追加で考えてみます。
直感的には、S → E → I → Rという形の遷移になります。つまり、感受性のある人 (S) は病原体に曝露され (E)、それが増えると感染状態 (I) になり、そして回復します (R)。
ここで増えた新しい遷移S → Eは、これまで考えてきたS → Iとprobability・rate・populationとも同じになります。また、IからRへの遷移が変わる理由もありません。
唯一変化があるのは、EからIへの遷移です。probabilityは1(Exposedの人全員が感染する)、populationはE(Exposedの人全員が感染する)、rateは変数δ(デルタ)とおくことにしましょう。

数式で表現するとこのようになります
$\frac{dE}{dt} = \beta・I・\frac{S}{N} - \delta・E$
$\frac{dI}{dt} = \delta・E - \gamma・I$
$\frac{dR}{dt} = \gamma・I$
SEIRモデルのシミュレーション
それではSEIRモデルのシミュレーションをしてみます。SIRモデルのシュミレーションは感染症のSIRモデル入門編 【シミュレーションコードあり】で紹介しましたが、今回のコードはその続きになります。
まずSEIRの常微分方程式の結果を返す関数を定義します。
def deriv(y, t, N, beta, gamma, delta):
S, E, I, R = y
dSdt = -beta * S * I / N
dEdt = beta * S * I / N - delta * E
dIdt = delta * E - gamma * I
dRdt = gamma * I
return dSdt, dEdt, dIdt, dRdt次にパラメーターを設定します。ここでは、100万人の集団を考え、ある感染症の潜伏期間が5日、感染持続期間が4日とし、1人の患者が5人に病原体を移す感染性の高い感染症だとします。
N = 1_000_000
D = 4.0 # 感染持続は4日
gamma = 1.0 / D
delta = 1.0 / 5.0 # 潜伏期間5日で割る
R_0 = 5.0
beta = R_0 * gamma # R_0 = beta / gammaなので、beta = R_0 * gammaとなる
S0, E0, I0, R0 = N-1, 1, 0, 0 # 最初は感染者が1人だけそれでは100日間のシミュレーションをしてみます。前回と同様、これはscipyを使えば簡単にできます。
t = np.linspace(0, 99, 100) # Grid of time points (in days)
y0 = S0, E0, I0, R0 # Initial conditions vector
# Integrate the SIR equations over the time grid, t.
ret = odeint(deriv, y0, t, args=(N, beta, gamma, delta))
S, E, I, R = ret.Tせっかくなので結果を可視化してみます。可視化する関数を
def plotseird(t, S, E, I, R, D=None, L=None, R0=None, Alpha=None, CFR=None):
f, ax = plt.subplots(1,1,figsize=(10,4))
ax.plot(t, S, 'b', alpha=0.7, linewidth=2, label='Susceptible')
ax.plot(t, E, 'y', alpha=0.7, linewidth=2, label='Exposed')
ax.plot(t, I, 'r', alpha=0.7, linewidth=2, label='Infected')
ax.plot(t, R, 'g', alpha=0.7, linewidth=2, label='Recovered')
if D is not None:
ax.plot(t, D, 'k', alpha=0.7, linewidth=2, label='Dead')
ax.plot(t, S+E+I+R+D, 'c--', alpha=0.7, linewidth=2, label='Total')
else:
ax.plot(t, S+E+I+R, 'c--', alpha=0.7, linewidth=2, label='Total')
ax.set_xlabel('Time (days)')
ax.yaxis.set_tick_params(length=0)
ax.xaxis.set_tick_params(length=0)
ax.grid(b=True, which='major', c='w', lw=2, ls='-')
legend = ax.legend(borderpad=2.0)
legend.get_frame().set_alpha(0.5)
for spine in ('top', 'right', 'bottom', 'left'):
ax.spines[spine].set_visible(False)
if L is not None:
plt.title("Lockdown after {} days".format(L))
plt.show();
if R0 is not None or CFR is not None:
f = plt.figure(figsize=(12,4))
if R0 is not None:
# sp1
ax1 = f.add_subplot(121)
ax1.plot(t, R0, 'b--', alpha=0.7, linewidth=2, label='R_0')
ax1.set_xlabel('Time (days)')
ax1.title.set_text('R_0 over time')
# ax.set_ylabel('Number (1000s)')
# ax.set_ylim(0,1.2)
ax1.yaxis.set_tick_params(length=0)
ax1.xaxis.set_tick_params(length=0)
ax1.grid(b=True, which='major', c='w', lw=2, ls='-')
legend = ax1.legend()
legend.get_frame().set_alpha(0.5)
for spine in ('top', 'right', 'bottom', 'left'):
ax.spines[spine].set_visible(False)
if Alpha is not None:
# sp2
ax2 = f.add_subplot(122)
ax2.plot(t, Alpha, 'r--', alpha=0.7, linewidth=2, label='alpha')
ax2.set_xlabel('Time (days)')
ax2.title.set_text('fatality rate over time')
# ax.set_ylabel('Number (1000s)')
# ax.set_ylim(0,1.2)
ax2.yaxis.set_tick_params(length=0)
ax2.xaxis.set_tick_params(length=0)
ax2.grid(b=True, which='major', c='w', lw=2, ls='-')
legend = ax2.legend()
legend.get_frame().set_alpha(0.5)
for spine in ('top', 'right', 'bottom', 'left'):
ax.spines[spine].set_visible(False)
plt.show()と定義すれば、
plotseird(t, S, E, I, R)とするだけでグラフを書くことができます。
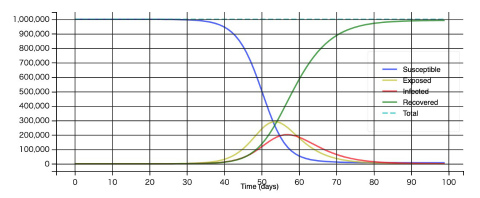
このように、基本再生産数=5という感染性がとても強い場合、100日後には100万人の集団全てにその感染が広まってしまうことになります。
Dコンパートメントの追加
残念ながら、感染症で亡くなる方も現実にはいらっしゃいます。
これまでのシミュレーションでは、感染後は全員回復するという仮定がありましたが、これは明らかに現実に即していません。そこで、感染後に回復するRコンパートメントだけでなく、感染後になくなってしまうDコンパートメントをモデルに追加していきます。
感染症にかかっている方が亡くなってしまうrateを表す新しい変数ρ(rho)を定義します(例えば、亡くなるまでに平均6日という場合、ρは1/6になります)。回復rate γについては、これまでのモデルと同じです。そのため、新しいモデルは次のようになります。

ここでまだ?になっているのは、感染Iから回復Rへのprobabilityと、感染Rから死亡Dへのprobabilityだけです。
これはもう一つの変数、死亡率αになります。例えば、α=1%だとすると、感染者のうち99%が回復する一方で、1%の方はなくなってしまうということを意味しています。これを導入すると、モデルはこのようになります。

この図を見ながら、次の連立方程式を直感的に書き下すことができます。
$\frac{dE}{dt} = \beta・I・\frac{S}{N} - \delta・E$
$\frac{dI}{dt} = \delta・E - (1-\alpha)・\gamma・I- \alpha・\rho・I$
$\frac{dR}{dt} = (1-\alpha)・\gamma・I$
$\frac{dD}{dt} = \alpha・\rho・I$
SEIRDモデルのpythonコード
それではこれを計算する関数を定義します。
def deriv(y, t, N, beta, gamma, delta, alpha, rho):
S, E, I, R, D = y
dSdt = -beta * S * I / N
dEdt = beta * S * I / N - delta * E
dIdt = delta * E - (1 - alpha) * gamma * I - alpha * rho * I
dRdt = (1 - alpha) * gamma * I
dDdt = alpha * rho * I
return dSdt, dEdt, dIdt, dRdt, dDdt各種パラメーターを設定します。死亡率はここでは5%としました。
N = 1_000_000
D = 4.0 # 感染は4日持続
gamma = 1.0 / D
delta = 1.0 / 5.0 # 潜伏期間は5日
R_0 = 5.0 # 1人の患者が5人に病原体を移す
beta = R_0 * gamma
alpha = 0.05 # 死亡率は5%
rho = 1/9 # 感染から死亡まで平均して9日
S0, E0, I0, R0, D0 = N-1, 1, 0, 0, 0 # 最初は1人のみ感染しているあとはいつもの通り時間点を作成し、scipyで計算するだけです。
t = np.linspace(0, 99, 100) # Grid of time points (in days)
y0 = S0, E0, I0, R0, D0 # Initial conditions vector
# Integrate the SIR equations over the time grid, t.
ret = odeint(deriv, y0, t, args=(N, beta, gamma, delta, alpha, rho))
S, E, I, R, D = ret.T図示もしておきます。
plotseird(t, S, E, I, R, D)
時間とともに変化するパラメーターの導入
これまでは、各コンパートメントに所属する人数だけが時間の経過とともに変化しました。しかしこれはとても非現実的です。さまざまなパラメーターも、時間とともに変化するからです。
例えば、ロックダウンをすれば1人の感染者が感染を広げる人数も減るでしょう。現実世界の感染の広がりをモデリングするためには、パラメーターを時間の経過とともに変化させる必要があります。
最初に簡単な変更をしてみます。L日目に厳格なロックダウンを実施し、R₀ を 0.9 にします。式では、R₀ではなくβを使用していますが、R₀ = β / γであるため、β = R₀ ⋅ γとなります。
N = 1_000_000
D = 4.0
gamma = 1.0 / D
delta = 1.0 / 5.0
def R_0(t):
return 5.0 if t < L else 0.9
def beta(t):
return R_0(t) * gamma
ロックダウンを開始するのは最初の感染から40日後としましょう。
L = 40 # 40日後にロックダウン開始残りはさきほどと全て同じです。
alpha = 0.05
rho = 1/9
S0, E0, I0, R0, D0 = N-1, 1, 0, 0, 0
t = np.linspace(0, 99, 100)
y0 = S0, E0, I0, R0, D0
ret = odeint(deriv, y0, t, args=(N, beta, gamma, delta, alpha, rho))
S, E, I, R, D = ret.T
plotseird(t, S, E, I, R, D, L)そうするとこのようになります。

L = 50だとどうなるでしょうか?
L = 50 # 50日後にロックダウン開始
ret = odeint(deriv, y0, t, args=(N, beta, gamma, delta, alpha, rho))
S, E, I, R, D = ret.T
plotseird(t, S, E, I, R, D, L)ロックダウン開始が10日遅れるだけで、感染の進行が全然違うことが分かります。

もちろん他のパラメーターも同様にして時間変化を組み込むことができます。
関連図書
この記事に関連した内容を紹介しているサイトや本はこちらです。
今日も【生命医学をハックする】 (@biomedicalhacks) をお読みいただきありがとうございました。当サイトの記事をもとに加筆した月2回のニュースレターも好評配信中ですので、よろしければこちらも合わせてどうぞ