人類の歴史は感染症との戦いの歴史でもあり、感染症が広まってしまうのかあるいは抑制できるのか、は常に大きな注目を集めてきました。
感染症の広がり方を予測する数学的なモデルが提唱され、SIRモデルと呼ばれています。
この記事では、SIRモデルの基本を高校レベルの微積分の知識までを使って説明し、Pythonを使ったシミュレーションの例を紹介します。
SIRモデルのパラメーター
感染症は、ある集団に所属する人から人へ広がる可能性があります。どのくらいの速さで広がるのか、どのくらいの割合で感染するのか、どのくらいの割合で死ぬのか、などについての洞察を得ようとしています。
感染症をモデル化する最も簡単な方法の一つが、コンパートメントモデルです。コンパートメントモデルは、例えば、集団をいくつかの区画、コンパートメントに分けます。
Susceptible: 感染する可能性がある(が、現時点では健康)
Infected: 感染した (まだ治っていない)
Recovered: 感染し、回復した(再び感染することない)
例えば、N=10000の人口、つまり10000人からなる集団を考えます。ある時刻t (例えば病気発生から7日後であれば、t=7日) において、400人が感染している場合、S(7) = 400と表現します。
SIRモデルでは、いくつかの初期パラメータを入力するだけで、すべての日tのS(t), I(t), R(t)の値を得ることができます。
新しい感染症Xがあったとします。この感染症では、感染者から健康な人に感染する確率は20%であるとします。
1日に接触する人の平均数は5人であるならば、1日に5人の人と接触し、それぞれの人が20%の確率で感染することになります。したがって、この感染者は1日に1人(20% ⋅ 5 = 1)に感染を移してしまいます。これがSIRモデルにおけるパラメーターβで、言い換えるとβは感染者が一日に感染させてしまう人数の期待値 (平均値)です。
これは1日あたりの人数ですので、日数が多くなれば感染者が増えていくことになります。例えば、日数D = 7とすると、この感染者は1日に1人に感染を移し、7日後には(1人/日 x 7日で)7人の新規感染者が出ることになります。
この指標が基本再生産数 (basic reproduction number) R₀と呼ばれるもので、1人の感染者が感染を移してしまう人の総数であり、当然ですがR₀ = β・Dという関係にあります。
あともう一つだけ、γを紹介させてください。γ = 1/Dとします。Dを感染者が感染症にかかっている日数と考えれば、γは1日あたりの感染者の回復率と考えることができます。
例えば、30人が感染していて、D=3(つまり3日間感染している)だとすると、1日あたりその1/3(つまり10人)の人が回復する計算になります。1/Dで定義されるγ (=1/3) が回復率だというのはそういうことになります。
先程のDの式を1/γにしただけですが確認のために示すと、R₀=β/γとなります。
SIRモデルの方程式
今度は、β、γ、Nだけで、全ての日におけるsusceptibleの患者数 S(t)、感染数 I(t)、回復者数 R (t)を求めたいとします。これらを直接求めるのは難しいものの、S,I,Rの1日あたりの変化を記述するのは簡単です。
感染症が発生してからt日たったとします。それでも、1人の感染者が1日に感染させる人数を1人(β=1)、感染者が病気を広げる日数は7日(γ=1/7、D=7)であるとしましょう。
仮に、t日目に60人が感染したとします(だからI(t)=60)、総人口は100人(N=100)、Susceptibleな状況にある人は30人(S(t)=30、R(t)=100-60-30=10)だとします。
この時、S(t)とI(t)とR(t)は翌日にどう変化するでしょうか?
60人の感染者がいて、それぞれ1日に1人ずつ感染を増やします(β=1)。しかし、彼らが出会った人のうち、30/100=30%の人だけがまだsusceptibleであり新規感染することがあります(S(t)/Nの計算をしています)。
だから、新規感染者は60・1・30/100=18人になります(1日平均1人に病原体を移すから60人に感染するのではなく、このうち3割にしか感染しないので、新規感染者は18人)。
この時、Susceptibleの30人のうち18人がInfectedになるので、S(t)はマイナス18の変化です。
ここまでの具体例での話を全部変数に戻せば、
関数の変化を表すのは微分であり、この場合はS'(t) と表記できます。
さて、感染者の量はどう変わるのでしょうか? まず新しい感染者については、Susceptibleの状態から変化してくる18人が該当するので、数式で書けば
です。また、感染状態から回復する人の存在も忘れてはなりません。60人が感染していて、γ=1/3なので、60人の3分の1が回復します。つまり、1/3 ⋅ 60 = 20です。回復者数をR'(t) とすれば
これらを合わせることで
右辺の第1項は、Susceptibleから新たに感染した人数で、第2項は回復者です。
回復者数の変化は、Infectedから移ってくる人だけですので、
最後に、これまで出した式をまとめておきます。
$\frac{dI}{dt} = \beta・I・\frac{S}{N} - \gamma・I$
$\frac{dR}{dt} = \gamma・I$
このような方程式を常微分方程式(ODE)と呼びます。
これで、感染しやすい人、感染した人、回復した人の数の変化を記述することができるようになりました。
PythonでSIRモデルをシミュレーション
それでは、今紹介したモデルをpythonのコードで表現してみます。インターラクティブな可視化ができるmpld3パッケージも使って、Google Colabで動かしていきます。
from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
!pip install mpld3
import mpld3
mpld3.enable_notebook()
上のグレーの網掛けで示した数式を計算し、まとめて結果を返す関数を定義します。
def deriv(y, t, N, beta, gamma):
S, I, R = y
dSdt = -beta * S * I / N
dIdt = beta * S * I / N - gamma * I
dRdt = gamma * I
return dSdt, dIdt, dRdt
1000人の集団で、そのうち1人だけ感染している状態からスタートしてみます。感染日数は4日、1日あたりに感染者1人が別の1人に病原体を移してしまうとします。
N = 1000
beta = 1.0 # 1人の感染者は1日に1人に病原体を移す
D = 4.0 # 感染は4日持続する
gamma = 1.0 / D
S0, I0, R0 = 999, 1, 0 # 初期条件、1人が感染していて、残り999人はSusceptible
微分方程式の難しいことは分からなくても、scipyの中にあるodeintを使えば簡単に計算できます。
t = np.linspace(0, 49, 50) # 50日の時間点を作成
y0 = S0, I0, R0 #初期条件をy0とする
# 時間点ごとにSIRモデルを計算する
ret = odeint(deriv, y0, t, args=(N, beta, gamma))
S, I, R = ret.T
これで、S, I, Rそれぞれの時間変化を計算できました。
せっかくなので、これをグラフで表現してみます。まずはグラフを作成する関数を定義します。
def plotsir(t, S, I, R):
f, ax = plt.subplots(1,1,figsize=(10,4))
ax.plot(t, S, 'b', alpha=0.7, linewidth=2, label='Susceptible')
ax.plot(t, I, 'y', alpha=0.7, linewidth=2, label='Infected')
ax.plot(t, R, 'g', alpha=0.7, linewidth=2, label='Recovered')
ax.set_xlabel('Time (days)')
ax.yaxis.set_tick_params(length=0)
ax.xaxis.set_tick_params(length=0)
ax.grid(b=True, which='major', c='w', lw=2, ls='-')
legend = ax.legend()
legend.get_frame().set_alpha(0.5)
for spine in ('top', 'right', 'bottom', 'left'):
ax.spines[spine].set_visible(False)
plt.show()
あとは、この関数に時間とS, I, Rの値を渡すことで簡単に作図ができます。
plotsir(t, S, I, R)
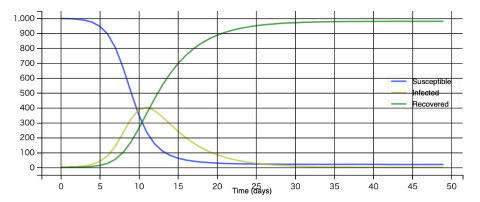
このシミュレーションでは、感染者のピークは11日後にやってきて、そのときの感染者数は400人に達します。また、50日の間に、最終的にほとんどの人が感染することも分かります。
このようにSIRモデルは便利ですが、やや単純すぎるところもあります。例えば、病原体に暴露した状態は反映されていませんし、感染した後に全員回復するとも限りません。
そうしたより現実世界に即したモデリングのためには、もう少し工夫が必要で、感染症のSIRモデル発展編 【数理モデルの拡張】でまとめています。
関連図書
この記事に関連した内容を紹介しているサイトや本はこちらです。
Google Colaboratoryでデータサイエンスを始めよう【使い方入門】
新型コロナウイルスのテクノロジーを使った対策 【予測・早期検出・治療】
今日も【生命医学をハックする】 (@biomedicalhacks) をお読みいただきありがとうございました。当サイトの記事をもとに加筆した月2回のニュースレターも好評配信中ですので、よろしければこちらも合わせてどうぞ









