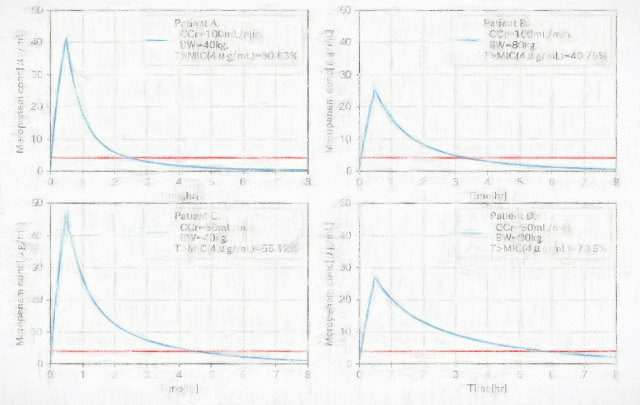
薬物動態をシミュレーションする方法【Rで簡単に計算できる】

血中薬物濃度を治療にふさわしい範囲に維持することは、薬物治療の基本です。

薬の投薬量や投薬経路、タイミングなどによってどのように血中濃度が変化していくのかは、微分方程式を使ったモデルを解くことで分かります。

成書にはそれらのモデルについて解説されているので、この記事では統計ソフトRのlinpkパッケージを使って簡単に薬物動態をシミュレーションする方法について紹介します。

この記事の内容

1 1コンパートメントモデルと1回の静脈内ボーラス投与
2 1コンパートメントモデルと点滴投与
3 1つのコンパートメントモデルと経口投与
4 複数回投与の場合
5 定常時の投与量
6 2コンパートメント, 3コンパートメント
7 さまざまなパラメーターを計算する
8 まとめに代えて
9 関連図書

1コンパートメントモデルと1回の静脈内ボーラス投与

まずは最も単純な1コンパートメントモデルに薬を1回静脈投与する場合のシミュレーションです。

1コンパートメントモデルについては1コンパートメントモデルと消失速度定数【簡単に薬物動態を計算する】でも紹介していますが、簡単にいうと、全ての薬が体内という1つの箱 (コンパートメント) に入り、その後に排出されるという単純なモデルです。

まず、薬物濃度をシミュレーションする時間点のベクトルを作成します。この例では、0時間から24時間までの等間隔の時間点のグリッドを作成してみます。

t.obs - seq(0, 24, 0.1) # 0から24時間まで0.1時間間隔でポイントを作成

ここでは、時間の単位はhourとしていますが、クリアランスと速度定数の単位が一致する限り、好きな時間単位を自由に使うことができます。例えば、時間の単位がdayで容積がLの場合、クリアランスはL/dayとなります。

次に、pkprofile関数を使用して、ある薬物のクリアランスを0.5 L/h, (中心コンパートメント) 分布容積が11 Lである薬物100 mgを静脈内投与した場合に各時点における濃度をシミュレーションします。

分布容積については分布容積と組織移行性を分かりやすく【計算方法と小さい・大きいの目安】で紹介しているので合わせてご覧ください。

y - pkprofile(t.obs, cl=0.5, vc=11, dose=list(amt=100))
plot(y)

ここで注意すべきことがいくつかあります。1つは、doseの引数がリストであるということです。

オブジェクトyは基本的には時間t.obsにおける濃度の数値ベクトルとして扱うことができますし、結果をdata.frameに変換することもできます。

sim - as.data.frame(y)
tail(sim)

1コンパートメントモデルと点滴投与

静脈内にボーラスで投与する場合のシミュレーションのやり方を見ましたが、これを輸液に変更するには、単に持続時間（durパラメーター）または輸液速度 (rateパラメーター) のどちらかをdose listの引数に追加するだけです。

例えば、先ほどと同じ薬100 mgを90分かけて注入する場合、次のようにします。

y - pkprofile(t.obs, cl=0.5, vc=11, dose=list(amt=100, dur=1.5))
plot(y)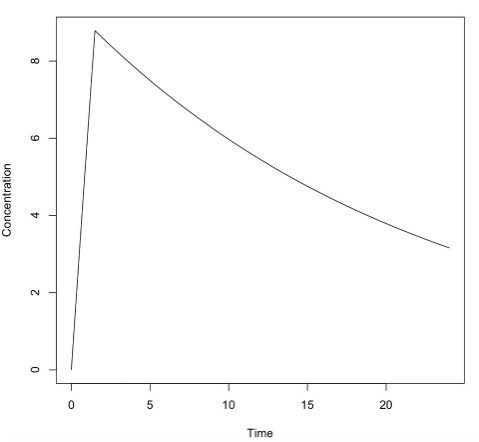

1つのコンパートメントモデルと経口投与

経口投与(つまり薬をdepot compartmentに投与)をシミュレートするためには、単純に吸収率定数kaを指定します。

y - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3, dose=list(amt=100))
plot(y)

投与量には関連するタイムlagとバイオアベイラビリティfもあります。投与量のうちのどれくらいのバイオアベイラビリティなどがあるかということを指定します。

経口投与してから0.4時間のラグがあり、バイオアベイラビリティは60%であるとすると

y - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3, dose=list(mt=100, lag=0.4, f=0.6))
plot (y)

複数回投与の場合

これまでは1回の投薬後のシミュレーションのやり方を見てきましたが、実際の薬は何回にも渡って投薬することの方が普通でしょう。

pkprofile関数に複数の投薬を指定するには、2つの方法があります。1つ目は dose のlist引数に投薬する時間を渡すことです。

例えば、1回目を時刻0, 2回目をその12時間後に投薬し、それぞれ100 mgを経口投与するなら

y - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3, dose=list(t.dose=c(0, 12), amt=100))
plot (y)

投与回ごとに異なる量を指定することもできます。例えば1回目を時刻0で100 mg投薬し、2回目をその12時間後に50 mgで投薬する場合は

y - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3, dose=list(t.dose=c(0, 12), amt=c(100, 50)))
plot (y)

データフレームを使って投薬量を指定することもできます。まずは投薬時間と投薬量についてのデータフレームを作成します。

doses - data.frame(t.dose=c(0, 12), amt=c(100, 50))
doses

t.dose amt
1 0 100
2 12 50
というデータフレームが用意できました。

このデータフレームをpkprofile関数に渡せば同じことができます。

y - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3, dose=doses)
plot (y)

複数の用量を指定する第2の方法は、追加投薬回数を表すaddl (additional) と、その投薬間隔 ii (inter-dose interval) を使う方法です。

例えば、12時間ごとに100 mgという投薬を5日間行う場合のシミュレーションは、初回投薬後に残り9回投薬することになるのでaddl = 9を指定して

t.obs - seq(0, 6*24, 0.5)
y - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3, dose=list(mt=100, addl=9, ii=12))
plot (y)

あるいはaddlを使わずにseq()を使って実際の投与時間をベクトルで指定しても同じことができます。

y - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3, dose=list(t.dose=seq(0, 9*12, 12), amt=100))
plot(y, col="red")

ここまでに見たさまざまなオプションを組み合わせることも可能です。例えば、24時間ごとに100 mgを投与し、3日目の14時間目に50 mgの追加投与を行う場合は

y - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3. dose=list(t.dose=c(0, 24*2 + 14), amt=c(100, 50), addl=c(4, 0), ii=24))
plot (y)

1つの薬は100 mgを時刻0に投薬して残り4回、もう1つの薬は時刻24*2 + 14に50 mgを投薬し残り0回、24時間ごとに繰り返して投薬するということを意味しています。

定常時の投与量

投与量リストの引数にss=Tまたはss=1を追加することで、定常状態での投与量を指定することができます。

例えば、先程の例で12時間ごとに100mgを5日間定期的に投与しました。5日後に定常状態に達したことを確認するために、定常状態のプロファイルを緑色で重ね合わせてみます。

t.obs - seq(0, 6*24, 0.5)
y - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3, dose=list(amt=100, addl=9, ii=12))
plot (y)
yss - pkprofile(t.obs, cl=0.5, vc=11, ka=1.3, dose=list(amt=100, addl=9, ii=12, ss=T))
lines(yss, col="green3")
legend("bottomright", c("定常状態"), col=c("green3"), lty=1, bty="n")

この時点で、定常状態である緑とシミュレーションが一致しており、薬物動態は定常状態に達していると判断できます。

2コンパートメント, 3コンパートメント

これまでは1コンパートメントモデルについて考えてきましたが、pkprofile関数では2、3コンパートメントモデルにも対応しています。

コンパートメントの数を指定するには、そのモデルに適したパラメータをpkprofile関数に含めることです。例えば2コンパートメントモデルの場合は，qとvpを追加します．

t.obs - seq(0, 24, 0.1)
y2 - pkprofile(t.obs, cl=0.5, vc=11, q=2, vp=30, ka=1.3, dose=list(amt=100))

3(またはそれ以上)コンパートメントモデルでは、qとvpをベクトルとして指定することができます。2コンパートメントモデルと合わせて図示してみます。

y3 - pkprofile(t.obs, cl=0.5, vc=11, q=c(2, 0.3), vp=c(30, 3), ka=1.3, dose=list(amt=100))
plot(y2)
lines(y3, col="green3")
legend("topright", c("2-compartment", "3-compartment"), col=c("black", "green3"), lty=1, bty="n")

2コンパートメントモデルでも3コンパートメントモデルでも大差ないということが分かります。

さまざまなパラメーターを計算する

これまでは薬物濃度のシミュレーションを見てきましたが、このデータを使ったさまざまなパラメーターも簡単に求めることができます。

例えば半減期を計算するにはhalflife関数を使うだけです。

先ほどの3コンパートメントモデルの半減期を求める場合、まずそのモデルを作成して、それをhalflife関数に渡します。

y - pkprofile(t.obs, cl=0.5, vc=11, q=c(2, 0.3), vp=c(30, 3), ka=1.3, dose=list(amt=100))
halflife (y)

これで3つのコンパートメントにおける半減期と、吸収半減期が表示されます。

最高血中濃度Cmaxや最高血中濃度到達時間Tmax, あるいはAUCといった、他の重要パラメーターはsecondary関数でまとめて計算できます。

secondary (y)

今回の例では、Cmaxが6.17, Tmaxが1.6, AUCが60.31になることが分かります。

これらのパラメータは各時間点のシミュレーション薬物濃度から計算されているので、t.obsで指定している時間点が重要な要素になります。

まとめに代えて

この記事では、薬物動態を簡単にシミュレーションできるRパッケージであるlinpkを紹介しました。

基本的にほとんどのことがpkprofile関数1つでできるという強力なメリットがある反面、線形微分方程式以外の複雑なPKモデリングには対応できないというデメリットもあります。

その場合、mrgsolve、PKPDsim、RxODEといった複雑な微分方程式を解くことができるRパッケージを使うことができます。

とはいえ多くの薬物動態シミュレーションはこのlinkpkパッケージのみで対応できるので、ぜひ使ってみてください。